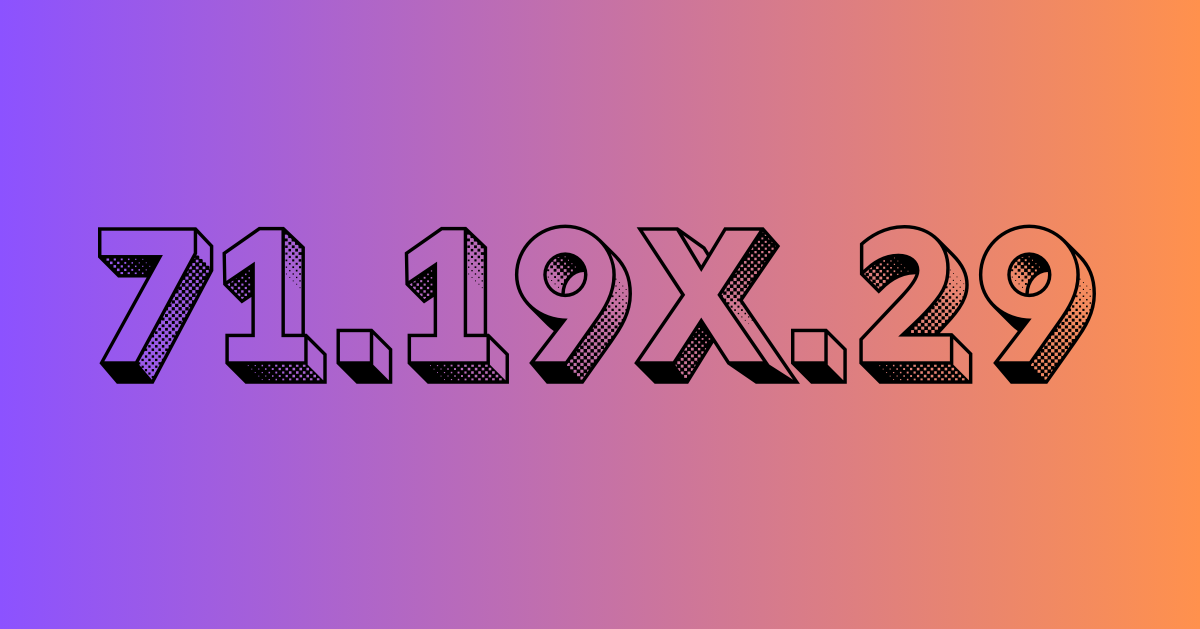Numbers hold immense significance in everyday life, from finance to science and engineering. However, their meaning can change drastically based on decimal placement. In the expression 71.19x.29, the decimal points determine the scale of each number, preventing misinterpretation or errors in calculations. Let’s explore the impact of decimals, their role in multiplication, and why accuracy matters.
The Importance of Decimal Placement
Decimals help define the size and accuracy of a number. Without them, values could be misunderstood entirely. For example, 71.19 and 7119 are vastly different, as are 0.29 and 29. A misplaced or missing decimal point could skew results, leading to significant miscalculations.
Breaking Down 71.19 × 0.29
To understand the expression 71.19 × 0.29, let’s analyze each component:
- 71.19 represents seventy-one and nineteen-hundredths.
- 0.29 represents twenty-nine hundredths, a fraction of one.
When multiplied, these values maintain their precision, ensuring accurate calculations.
Multiplication of Decimals: Step-by-Step Approach
When multiplying decimals, follow these steps:
Ignore the decimal points temporarily and multiply as if working with whole numbers.
Multiply 7119 by 29:
7119 × 29 = 206451
Count the decimal places in the original numbers:
71.19 has two decimal places
0.29 has two decimal places
The total decimal places in the result should be four.
Place the decimal in the final product:
2064.51 (correctly adjusted).
Thus, 71.19 × 0.29 = 20.6451.
Real-World Applications of Decimal Precision
1. Finance and Economics
Decimals are crucial in financial transactions. If a decimal is misplaced in currency calculations, it could mean the difference between $20.64 and $2064—a costly mistake!
2. Science and Engineering
In physics and engineering, decimal precision ensures accurate measurements. A slight miscalculation in scientific data could alter an experiment’s outcome significantly.
3. Medicine and Dosage Calculations
Medical professionals rely on precise decimal placement in drug dosages. An incorrect decimal shift could result in overdosing or underdosing, leading to severe consequences.
Why Precision in Mathematics Matters
Mathematical accuracy isn’t just about getting the right answer—it’s about ensuring reliability across different fields. Whether in accounting, engineering, or daily transactions, decimal placement safeguards against critical errors.
Common Mistakes When Working with Decimals
- Ignoring decimal placement and treating numbers as whole values.
- Misplacing the decimal in final answers, altering results.
- Rounding too early, leading to loss of precision.
- Skipping the step of counting decimal places when multiplying.
Tips to Avoid Decimal Errors
- Always double-check decimal placement when performing calculations.
- Use a calculator or software for high-precision work.
- Practice mental estimation to verify if results seem reasonable.
- Ensure consistent rounding rules in financial and scientific applications.
Conclusion
The expression 71.19 × 0.29 = 20.6451 demonstrates how decimal placement accuracy mathematical precision. In finance, science, and daily life, ensuring accurate decimal positioning prevents costly errors and enhances reliability. Understanding decimal multiplication is not just about numbers—it’s about making precise decisions in every aspect of life.
FAQs
What happens if I misplace a decimal when multiplying?
Misplacing a decimal can drastically change the result, leading to significant miscalculations, especially in finance and medicine.
Why does 71.19 × 0.29 have four decimal places in the answer?
The total number of decimal places in the product is the sum of decimal places in both factors (2 from 71.19 and 2 from 0.29).
Can I round the result of 71.19 × 0.29?
Yes, depending on context. For financial transactions, rounding to two decimal places (20.65) might be suitable, while scientific applications may require more precision.
What are some common real-life scenarios where decimal precision matters?
Banking transactions, engineering measurements, scientific experiments, and medical dosages all rely on accurate decimal placement.
How can I improve my accuracy with decimals?
Practice regularly, use estimation techniques, and double-check decimal placements when performing calculations manually.